2022-02-07 11:36:28 文章来源:未知

2023国考行测数量关系之三角形“魔咒”怎么破?
2023国考行测数量关系之三角形“魔咒”怎么破?
在国考行测数量关系模块中,几何问题是每年必考内容。通过统计近几年的几何问题可以发现在几何问题中三角形备受出题人青睐。具体细化来看,特殊三角形比如直角三角形、等腰三角形、相似三角形等都是经常出题的模型,这些三角形的基本性质在初中时都有涉及到,只要大家进行全面的回顾就可以掌握这类题目。下面,我们就来对直角三角形和相似三角形进行一个系统的回顾。

一、直角三角形
![]()
有一种特殊的直角三角形,即直角三角形中两个锐角分别为60°和30°。假设斜边为a,30°所对应的直角边为b,60°所对应的直角边为c,那么边长之间的关系为b=a/2,。这个结论需要大家直接记住,以便做题的时候能够更节省时间。下面我们来看一道真题。

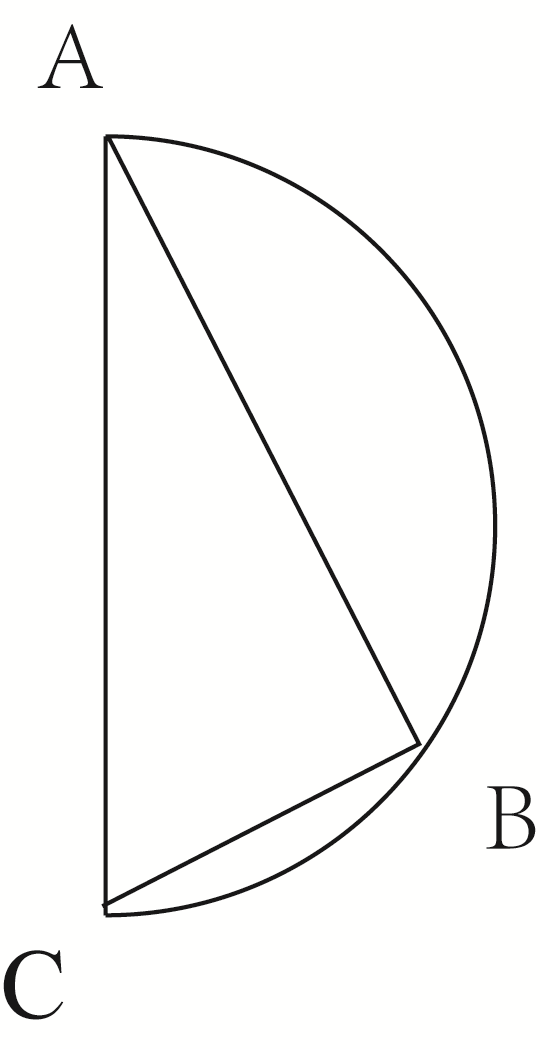
【例】如下图所示,甲和乙在面积为54π的半圆形游泳池内游泳,他们分别从位置A和B同时出发,沿直线同时游到位置C,若甲的速度为乙的两倍,则原来甲乙两人相距( )。
![]()
A.米 B.15米
![]()
C.米 D.18米
![]()
【解析】甲从位置A出发到位置C,走的距离为AC,乙从位置B出发到位置C,走的距离为BC。求原来甲乙两人的距离,即求AB。直径所对的圆周角是直角,即角B为直角。根据行程公式S=Vt,同时出发同时到C,所用的时间相同,甲的速度为乙的速度的两倍,则甲走的距离为乙走的距离的两位,即AC=2BC。从而可以推断角A为30°,角C为60°,那么AB=AC/2。半圆形的面积的πr2/2=54π,求得r=6米,AC=12米,所以AB=18米。故本题正确答案为D选项。
二、相似三角形
相似三角形是近几年来出题的一个热点。首先大家要先清楚相似三角形的判定,基本上判定方法可以简述为以下四种。
(1)平行于三角形一边的直线和其他两边所构成的三角形与原三角形相似;
(2)两边对应成比例且夹角相等,两个三角形相似;
(3)三边对应成比例,两个三角形相似;
(4)两角对应相等,两个三角形相似。
根据这四条判断定理确定为相似三角形后,更多时候是利用相似三角形对应边成比例来进行做题。下面我们来看一道真题。
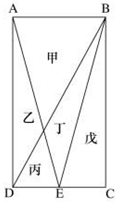
【例】一块种植花卉的矩形土地如图所示,AD边长是AB的2倍,E为CD边的中点,甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。问种植白花的面积占矩形土地面积的()。
A.3/4 B.2/3

C.7/12 D.1/2
![]()
【解析】将AD赋值为4,AB赋值为2,矩形土地的面积为4*2=8。种植百花的分别为甲区域和戊区域,戊区域的面积=1*4*=2。甲区域与丙区域为相似三角形(角对应相等),则对应边成比例。设甲区域的高为a,丙区域的高为b,则a/b=2/1,,甲区域的面积=。所以种植白花的面积占矩形土地面积的。故本题正确答案为C选项。
通过这两个题目的讲解,想必大家对直角三角形和相似三角形的考查有了一定的了解,但是题目的形式多种多样,还需要大家多做题目,强加练习,这样在考试的时候遇到三角形类的几何问题才能游刃有余。
相关内容推荐:
信息汇总——2025国考公告预约 | 职位检索 | 历年进面分数线
| 职位检索 | 历年进面分数线
辅导课程—— 2025国考系列课程 | 在线咨询
2025国考系列课程 | 在线咨询

企业微信客服

山东华图微信公众号