2022-05-13 17:26:00 文章来源:未知

2023国家公务员考试:资料分析之逆向思维求解概率问题
2023国家公务员考试:资料分析之逆向思维求解概率问题
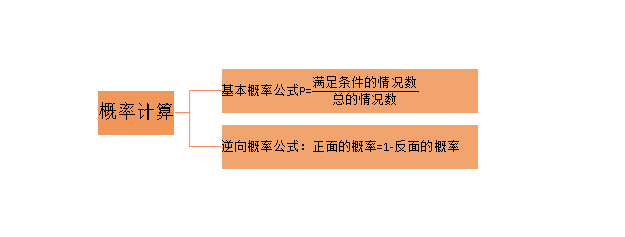
概率问题在我们的公考中非常常见,它是反映随机事件出现的可能性大小,通常喜欢与排列组合问题结合起来考察大家。学过数学中的概率问题,我们大家都知道要求一件事情发生的概率,可以用这个公式:事件发生的概率P=满足条件的情况数÷总的情况数,来计算所要求的概率,但题目中经常会出现一类题,正面去求解概率会相对复杂,比如一个简单的扔硬币的例子:

例:连续扔3次硬币,至少一次是正面向上的概率?
![]()
解析:至少一次是正面向上,那就意味着有可能是1次、也有可能是2次、也有可能是3次正面向上,需要分别去讨论每一种情况,相对来说比较复杂。如果我们换个思路,至少一次正面向上它对应的反面情况就是3次都是背面向上,那么我们就可以一步求出3次都是背面向上的概率为,总的概率是1,用总的概率减去背面向上的概率即为所求概率,即可得至少一次正面向上的概率是7/8。
通过这个小例子不难发现,正面思考情况比较复杂时,可以尝试逆向思考,节省时间又不容易出错。

给大家总结一个公式:正面的概率=1-反面的概率,在概率问题中正向考虑较为复杂时应用。看几道真题细品一下:
(2020年浙江)某公司对10个创新项目进行评选,选出最优秀的3个项目投入运行。小张随机预测3个项目将会入选。问他至少猜对1个入选项目的概率在以下哪个范围内?
A. 不到50%
B. 50%~60%
C. 60%~70%
D. 超过70%

【解析】第一步,本题考查概率问题,属于基本概率类。
![]()
第二步,本题问至少猜对1个入选项目的概率为多少,正面求解较为困难,从反面求解,至少猜对1个的概率=1-全猜错的概率。总的情况数为从10个中任意挑选三个,情况数为,全猜错的情况为从错误的七个里面任意挑选三个,情况数为,全猜错的概率为,因此至少猜对一个的概率为。
因此,选择D选项。
(2021年浙江)研究人员在A、B、C、D、E五块试验田中种植甲、乙、丙、丁、戊五种作物,每块试验田只种一种作物,每年都在所有的安排中随机挑选一种进行种植。问在连续的3年中,A试验田至少2年种植同一种作物的概率为:
A.36%
B.48%
C.52%
D.64%

【解析】第一步,本题考查概率问题。
![]()
第二步,正向求解情况数较多,考虑逆向概率,A试验田至少2年种植同一种作物的逆向是A试验田每年种植的作物都不相同,分步考虑,第一年A试验田种植任意一种都可以,概率为1,第二年种植作物不能跟第一年相同,概率为,第三年种植作物不能跟前两年相同,概率为,故A试验田每年种植的作物都不相同的概率为,A试验田至少2年种植同一农作物的概率为1-48%=52%。
因此,选择C选项。
相关内容推荐:
信息汇总——2025国考公告预约 | 职位检索 | 历年进面分数线
| 职位检索 | 历年进面分数线
辅导课程—— 2025国考系列课程 | 在线咨询
2025国考系列课程 | 在线咨询

企业微信客服

山东华图微信公众号