2022-09-28 11:45:24 文章来源:未知

2023国考数量关系之灵活性强的几何问题
2023国考数量关系之灵活性强的几何问题
在历年国家公务员考试当中,数量关系这一模块总是让无数考生望而生畏,从而产生放弃的想法。根据国家公务员考试的考情,数量关系按照省部级和地市级两套卷出题量一般是15道和10道,要求考生在短时间甚至是一分钟之内得出答案,确实很难,所以考生一定要学会一些解题技巧和做题原则,快速地选出正确答案,尽可能的多得分。
数量关系里边涉及到的题型有很多,我们今天就来聊一聊其中一个我们比较熟悉而且灵活性比较强的题型-几何问题。首先我们先来了解一下几何问题在国家公务员考试中的考情:2016年至2021年这6年的国家公务员考试中几何问题有5年都出现在考试试卷上,其中也不乏一套试卷出现两三道几何问题的,并且几何问题灵活多变涉及到的公式、特性等又比较多,所以考生一定要重视几何问题。学习几何问题一定要先了解里边涉及到的题型和知识点,几何问题的知识点思维导图如下:
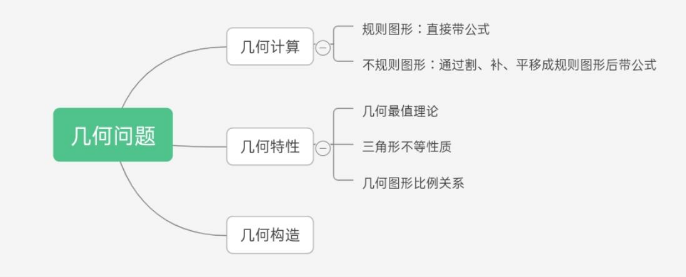
下边我们可以通过几道例题来感受一下几何问题在考试中的具体呈现:
【例1】如图所示,周长为24米的平行四边形绿化地被划分为三块区域,两边为三角形的花坛,中间为矩形的草地。已知a、b、c长度之比为4∶2∶√3,则矩形草地的面积为( )平方米。
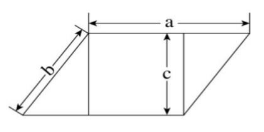
A.6 B.6√3
C.12 D.12√3
【解析】本题考查几何问题,由题意可得平行四边形周长是24米,所以2×(a+
b)=24,a+b=12,又因为a、b、c长度之比为4∶2∶√3,所以a=8,b=4,c=2√3。如下图所示,已知m=4,c=2√3,根据直角三角形三边的关系可得两边的三角形是有30°角的直角三角形,所以n=2,矩形的面积=(8-2)×2√3=12√3(平方米)。因此,选择D选项。
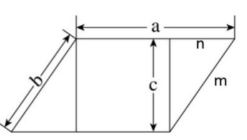
【例2】边长为整数且成等差数列的三个正方形,面积之和不大于5000,其中有两个正方形的面积之和等于第3个正方形的面积,这样的正方形存在多少组?
A.6 B.7
C.9 D.10
【解析】本题考查几何问题,根据题意可设三个正方形的边长分别是a+n、a、a-n(a、n均为正整数),所以(a+n)2+a2+(a−n)2≤5000,化简得:3𝑎2+2𝑛2≤5000。又因为a2+(a−n)2=(a+n)2,所以a2=4𝑎𝑛,a=4n。结合前边的结论可得3×16𝑛2+2𝑛2=50𝑛2≤5000,所以𝑛2≤100,n的取值区间是[1~10],所以共有10组满足题意的正方形存在。因此,选择D选项。
【例3】一个长方形长6cm,宽4cm,现分别平行于长和宽剪了若干刀,将长方形分若成若干个小长方形,这些小长方形的周长之和比原长方形周长多了56cm。那么最多剪了( )刀。
A.3 B.4
C.5 D.6
【解析】本题考查几何问题,由题意可得每平行于长方形的长剪一刀增加周长12cm,每平行于长方形的宽剪一刀增加周长8cm。因为小长方形的周长之和比原长方形周长多了56cm,要想尽可能的多剪,则多平行于长方形的宽去剪。设平行于长方形的长剪了x刀,平行于长方形的宽剪了y刀,可得:12x+8y=56,化简得:3x+2y=14,因为x、y均为正整数且根据奇偶特性x为2的倍数,为了能多剪几刀让x尽可能的小,y尽可能的大。当x=2时,y=4,满足题意,所以最多剪了2+4=6(刀)。因此选择D选项。
通过这三道例题大家就可以感受到,几何问题会和其他的知识点进行杂糅来增加难度,所以要想学好几何问题除了基础的公式和特性需要熟练掌握外,还要学会和其它知识点
进行灵活地结合运用,这样我们才能胜券在握,一举得分,成功上岸!
相关内容推荐:
信息汇总——2025国考公告预约 | 职位检索 | 历年进面分数线
| 职位检索 | 历年进面分数线
辅导课程—— 2025国考系列课程 | 在线咨询
2025国考系列课程 | 在线咨询

企业微信客服

山东华图微信公众号