您当前位置：山东人事考试 > 国家公务员考试 > 备考技巧 > 行测 > 2023国考数量关系之比例法巧解行程问题

2023国考数量关系之比例法巧解行程问题

2022-10-25 17:23:33 文章来源：未知

公告汇总

刷题资料

网络课程

在线咨询

点击订阅

山东华图

公务员招录，事业单位考试，医疗卫生

2023国考数量关系之比例法巧解行程问题

行程问题是数量关系中较为常见的一种题型，不少小伙伴感觉行程问题较难，原因是行程问题的过程可以描述的较为复杂，而且模型众多题型变化也较多。大家有时会发现单纯地使用方程法和赋值法解题较为复杂，今天小编就来带大家学习一下比例法在行程问题中的应用。

一、什么是比例法：

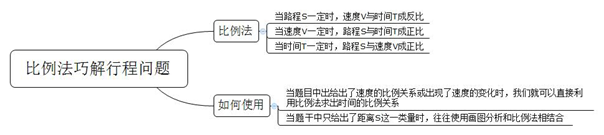
根据行程问题的基本公式S=V×T可知这三个量的比例关系：

1.当路程S一定时，速度V与时间T成反比;

2.当速度V一定时，路程S与时间T成正比;

3.当时间T一定时，路程S与速度V成正比。

二、什么情况下使用比例法解题较为方便：

1.当题目中出给出了速度的比例关系或出现了速度的变化时，我们就可以直接利用比例法求出时间的比例关系，再进一步求解。当题中给出时间的比例关系时，也可以直接得出速度的比例关系。

2.当题干中只给出了距离S这一类量时，使用画图分析法和比例法相结合往往可以快速解题。

三、实战演练：

例1. 一架战斗机从甲机场匀速开往乙机场，如果速度提高25%，可比原定时间提前12分钟到达，如果以原定速度飞行600千米后，再将速度提高三分之一，可以提前5分钟到达。那么甲乙两机场的距离是多少千米?

A. 750

B. 800

C. 900

D. 1000

【思路点拨】本题正确答案为C选项。题干中出现了速度的变化，可以知道变化前后的速度比，进而求出时间比，就能求出总的时间。设原速度为v千米/分钟。根据路程相等时，速度之比等于时间的反比，由v∶(1+25%)v=4∶5，则时间之比为5∶4，故时间差1份，由“提前12分钟到达”可知1份时间为12分钟，原速度飞行的时间为5份，则按原速度飞行需要60分钟，所以总路程为60v。

同理，在第二次运动中变速的部分路程为60v-600，原来的速度与变速后的速度比为v∶(1+)v=3∶4，可得时间之比为4∶3，则时间差为1份，即5分钟，则4份时间为20分钟。则按原速度飞行60v-600的路程需要20分钟，而且按原速飞全程需要60分钟，那么行驶600千米就需要60-20=40分钟。则总时间60分钟可飞行900千米，即全程。

例2.一条圆形跑道长500米，甲、乙两人从不同起点同时出发，均沿顺时针方向匀速跑步。已知甲跑了600米后第一次追上乙，此后甲加速20%继续前进，又跑了1200米后第二次追上乙。问甲出发后多少米第一次到达乙的出发点?

A. 36

B. 37

C. 39

D. 41

【思路点拨】本题正确答案为D选项。本题只给出了路程这一类具体值，考虑使用比例法。从第一次甲追上乙到第二次追上，甲比乙多走500米，那么乙走了1200-500=700(米)，则甲乙速度之比就等于路程之比，为12∶7。根据比例赋值甲的提速后的速度为12，乙的速度为7，那么原来甲的速度为=10，则第一次追及甲乙走过的路程比为10∶7。根据甲走了600米，可推出乙走了600×=420(米)，甲比乙多走了600-420=180(米)，即甲乙初始时相距180米，那么甲走180米第一次到达乙的出发点。