2023-07-17 14:51:41 文章来源：未知
2024年国考行测备考干货之数字特性法
数量关系一直是多数考生比较头疼的一个模块，因为数量太难使得许多考生心生畏惧，但是数量关系也会存在部分的题目可以进行秒杀。今天，图图就如何使用数字特性法进行秒杀给大家支支招。
一、奇偶特性：
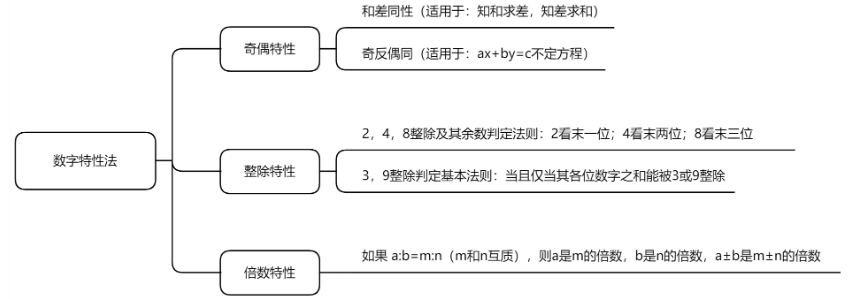
1.和差同性(适用于：知和求差，知差求和)
任意两个数的和如果是奇数，那么差也是奇数。
任意两个数的和如果是偶数，那么差也是偶数。
2.奇反偶同(适用于：ax+by=c不定方程)
任意两个数的和或差是奇数，两数奇偶相反。
任意两个数的和或差是偶数，两数奇偶相同。
例1.方程px+q=99的解为x=1，p、q 均为质数，则 p×q的值为：
A.194
B.197
C.135
D.155
【答案】A
【解析】第一步，本题考查基础应用题，用数字特性法解题。
第二步，根据“方程p+q=99的解为 x=1”得p+q=99，因为结果为奇数，根据奇反偶同可知p和q为一奇一偶。又因为“p、q 均为质数”所以p和q有一个数既为偶数又为质数。
第三步，已知2是唯一一个既为质数又为偶数的数，所以p和q有一个为2,假如p=2，则q=97，则p×q=2×97=194。
因此，选择A选项。
例2. 某次测验有50道判断题，每做对一题得3分，不做或做错一题倒扣1分，某学生共得82分，问答对题数和答错题数(包括不做)相差多少?
A.33
B.39
C.17
D.16
【答案】D
【解析】第一步，本题考查基础应用题，用数字特性法解题。
第二步，试卷有50道判断题，对+不做或错=50(偶数)，根据奇偶特性中的和差共性可得，对-不做或错=偶数，四个选项只有D选项为偶数，因此选择D选项。
因此，选择D选项。
二、整除特性：
2，4，8整除及其余数判定法则
一个数能被2(或者5)整除，当且仅当末一位数字能被2(或者5)整除;
一个数能被4(或者25)整除，当且仅当末两位数字能被4(或者25)整除;
一个数能被8(或者125)整除，当且仅当末三位数字能被8(或者125)整除。
3，9整除判定基本法则
一个数字能被3整除，当且仅当其各位数字之和能被3整除;
一个数字能被9整除，当且仅当其各位数字之和能被9整除。
例3. 现有5盒动画卡片，各盒卡片张数分别为：7、9、11、14、17。卡片按图案分为米老鼠、葫芦娃、喜
羊羊、灰太狼4种，每个盒内装的是同图案的卡片。已知米老鼠图案的卡片只有一盒，而喜羊羊、灰太狼图案的卡片数之和比葫芦娃图案的多1倍，那么图案为米老鼠的卡片的张数为：
A.7
B.9
C.14
D.17
【答案】A
【解析】第一步，本题考查基础计算问题，用数字特性法解题。
第二步，5盒动画卡片共有7+9+11+14+17=58(张)，喜羊羊、灰太狼图案的卡片之和比葫芦娃图案多1倍，即是葫芦娃图案的2倍。那么喜羊羊+灰太狼+葫芦娃=3×葫芦娃，即喜羊羊+灰太狼+葫芦娃的卡片数是3的倍数，喜羊羊+灰太狼+葫芦娃的卡片数=总数-米老鼠的卡片数，那么总数-米老鼠的卡片数能被3整除。
第三步，代入选项验证，A选项，58-7=51，能被3整除;B选项，58-9=49，不能被3整除，排除;C选项，58-14=44，不能被3整除，排除;D选项，58-17=41，不能被3整除，排除。只有A选项满足题意。
因此，选择A选项。
三、倍数特性：
如果(m和n互质)，则a是m的倍数，b是n的倍数，a±b是m±n的倍数
例4. 某中学高一至高三年级的学生参加某项社区服务，如果高三年级与高一年级、高三年级与高二年级参加此活动的人数之比分别为5∶3、8∶5，则该中学高一至高三年级最少共有( )人参加该项社区服务。
A. 40
B. 55
C. 79
D. 89
【答案】
【解析】第一步，本题考查基础计算问题，用数字特性法解题。
第二步，将高三作为中间量(5和8的最小公倍数为40)，则高三∶高一=5∶3=40∶24;高三∶高二=8∶5=40∶25;可得三个年级人数比为高一∶高二∶高三=24∶25∶40。
第三步，根据倍数特性：“如果(m和n互质)，a±b是m±n的倍数” 则该中学高一至高三年级的人数是24+25+40=89的倍数，即最少有89人参加该项社区服务。
因此，选择D选项。
四、总结：
以上四个题通过使用数字特性使得我们解题的时间大大减少，做题的效率和效果得到了较大的提高。数字特性的基本原理相对简单，我们需要做的是在日后的刷题过程中，一定要有意识的去培养用数字特性的思维来解题，找到那个捷径，从而在短时间内快速破题。
相关内容推荐：
信息汇总——2024国考公告专题
| 职位检索 | 历年进面分数线
笔试课程——
2024国考笔试课程 | 
国考交流群 | 在线咨询
企业微信客服
山东华图微信公众号
