2023-07-24 16:08:31 文章来源：未知
2024国考资料分析技巧：几个重要基期量的速算
基期量包含基期量，基期量之差，基期比重，基期倍数，基期平均数等相关量，本专题主要是介绍使用同一个公式计算的基期量，就是基期比重，基期倍数和基期平均数的速算方法。
对于材料中，给出现期量和增长率，进而求基期比重，基期倍数，基期平均数，均可利用公式：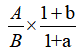
，然而能用这个公式计算的基期量，主要难度在于计算量大。因此对于这样的式子，如何快速计算呢?这是需要我们结合式子本身与选项差距，进行有效判断。总的来说，分两种情况，一般情况下，能用第一种方式，就不考虑第二种速算方式，因为第二种方式计算量稍大。
| 判断原则 | 速算方法 | |
| 方式一 | a与b差距小，即 ≈1 |
精算： ，根据 大小判断方向，差距小于|a-b| |
| 方式二 | a与b差距大 | 利用： |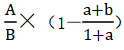
注意：若
<1，使用方式一是准确的，即通过利用差距小于∣a-b∣进行大小判断，但是若
>1，则差距将会大于∣a-b∣，或者直接用方式二进行速算即可。
具体如何操作，下面通过三个例子进行详细讲解：
【例1】(2019深圳)2018年1-9月汽车行业统计数据如下：
乘用车累计产销分别完成1735.1万辆和1726.0万辆，同比分别增长0.1%和0.6%。中国品牌乘用车累计销售724.2万辆，同比下降1.5%。
2017年1—9月，中国品牌乘用车销量占乘用车销量的比重是( )。
A.41.9% B.42.9%
C.44.1% D.46.2%
【答案】B
【解析】第一步，本题为基期比重计算。
第二步，依据基期比重公式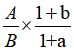
，定位材料A为724.2万辆，a为-1.5%，B为1726.0万辆，b为0.6%，代入公式得
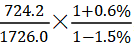，精算
=41.9%，因为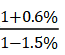
>1，差距且小于|a-b|=|-1.5%-0.6%|=2.1%。
因此，本题选择B选项。
【例2】(2021联考)
截至2019年12月31日，中国共产党党员总数为9191.6万名，同比增长1.46%。2019年共发展党员234.4万名，比上年增长14.06%。
2018年，发展党员数占同期党员总数的比例约为( )
A.1.8% B.2.3%
C.2.7% D.3.2%
【答案】B
【解析】第一步，本题为基期比重计算。
第二步，依据基期比重公式
，定位材料数据，A为234.4万名，a为14.06%，B为9191.6万名，b为1.46%，代入公式得
，因为a与b差距大，而选项差距小，因此原式转为
，而选项首位相同，第二位不同
，采用直除法，分母保留三位进行计算，即为
≈2.6%，因此原式=
≈2.6%-0.3%=2.3%。
因此，本题选择B选项。
【例3】(2020北京)
2017年全国共有各级各类民办学校17.76万所，占全国学校总数34.57%;各类民办教育在校生达5120.47万人，比上年增长6.12%。其中：民办普通高中3002所，比上年增长7.71%;在校生306.26万人，比上年增长9.74%。民办中等职业学校2069所，比上年下降2.17%;在校生197.33万人，比上年增长7.16%。
2016年平均每所民办中等职业学校在校生人数约为( )
A.871人 B.991人
C.1091人 D.1181人
【答案】A
【解析】
第一步，本题我基期平均数计算
第二步：基期平均数公式为：
，定位材料数据，可知A为197.33万人，a为7.16%，B为2069所，b为-2.17%，代入公式得
，观察选项，首位相同，第二位不同，
考虑分母四舍五入保留三位，即
≈95，即首两位为95，而
<1，即答案首两位小于95。
因此，本题选择A选项。
上述3个例题，介绍了基期比重和基期平均数的速算方式，而基期倍数也是使用
，因此，速算方法是一致的。希望各位考生认真理解然后多练习巩固。
相关内容推荐：
信息汇总——2025国考公告预约
| 职位检索 | 历年进面分数线
辅导课程——
2025国考系列课程 | 在线咨询
企业微信客服
山东华图微信公众号
