您当前位置：山东人事考试 > 国家公务员考试 > 备考技巧 > 行测 > 2024国考行测数量关系技巧：设未知数轻松解决方程问

2024国考行测数量关系技巧：设未知数轻松解决方程问题

2023-10-16 13:20:57 文章来源：未知

公告汇总

刷题资料

网络课程

在线咨询

点击订阅

山东华图

公务员招录，事业单位考试，医疗卫生

2024国考行测数量关系技巧：设未知数轻松解决方程问题

　　2024国考行测数量关系技巧：设未知数轻松解决方程问题

　　在历年的国家公务员行测考试中，方程法一直数量关系使用最多的方法，在2021年国考的题目中，有10道以上的题目可以用到方程法，对于一些题型来说，如果不能巧妙的设未知数的话，做题相对比较麻烦，如果在方程类的题目中能够巧妙设未知数，会让解题变的较为简单，考场得分相对比较容易。下面就让我们一起先来学习下方程法的设未知数的几个原则：

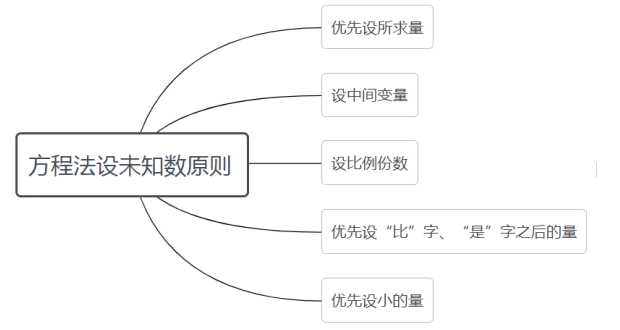
设未知数的原则	（1）在同等情况下，优先设求的量（即求谁设谁）
	（2）设中间变量（缺谁设谁）
	（3）按比例份数设未知数（有分数、百分数、比例倍数）
	（4）优先设“比”、“是”等关键字后面的量
	（5）优先设小的量

　　接下来我们通过3道题来具体看一下在题目中怎么使用这几个设未知数的技巧。

　　【例1】出租车队去机场接某会议的参会者，如果每车坐3名参会者，则需另外安排一辆大巴送走余下的50人;如果每车坐4名参会者，则最后正好多出3辆空车。问该车队有多少辆出租车?( )

　　A.50 B.55

　　C.60 D.62

　　【答案】D

　　【解析】第一步，本题考查基础应用题，方程法解题。

　　第二步，设该车队共有x辆出租车，根据参加会议的参会者总数不变，可得方程：3x+50=4(x-3)，解得x=62。

　　因此，选择D选项。

　　【例2】在一场篮球比赛中，甲、乙、丙、丁共得125分，如果甲再多得4分，乙再少得4分，丙的分数除以4，丁的分数乘以4，则四人得分相同。问甲在这场比赛中得了多少分?( )

　　A.24 B.20

　　C.16 D.12

　　【答案】C

　　【解析】第一步，本题考查基础应用题，用方程法解题。

　　第二步，本题我们如果说直接设甲的得分的话，则乙、丙、丁的分数不太好表示，但是我们发现甲、乙、丙、丁的分数都和相同得分产生了关系，则这个相同得分就相当于中间变量，则设相同得分为x，则原来甲得分为x-4，乙得分为x+4，丙为4x，丁为x/4，根据甲、乙、丙、丁共得125分，可得x-4+x+4+4x+x/4=125，解得x=20。

　　第三步，故甲原来得分为20-4=16(分)。

　　因此，选择C选项。

　　【例3】某有色金属公司四种主要有色金属总产量的1/5为铝，1/3为铜，镍的产量是铜和铝产量之和的1/4，而铅的产量比铝多600吨。问该公司镍的产量为多少吨?( )

　　A.600 B.800

　　C.1000 D.1200

　　【答案】A

　　【解析】第一步，本题考查基础应用题，用方程法解题。

　　第二步，根据有色金属总产量的1/5为铝，1/3为铜，可得总产量既是3的倍数又是5的倍数，因此设总产量为15x(3和5的公倍数)，则铝为3x，铜为5x。可推出镍为(5x+3x)×1/4=2x，则铅为15x-3x-5x-2x=5x。根据铅的产量比铝多600吨，得到5x-3x=600，即2x=600，所以镍为600吨。

　　因此，选择A选项。

　　总结：从以上3道题我们可以看到，方程法的题目一般难度不会特别大，但是在设未知数时能够掌握一定的技巧，并且能够灵活运用，这样在考场上就会起到事半功倍的效果。