2024国考资料分析计算干货化除为乘进阶运用

2024国考资料分析计算干货化除为乘进阶运用

很多同学学习了化除为乘之后很少用起来，原因是没有掌握化除为乘的进阶运用，当各位掌握了进阶运用，适用范围就比较广了，可以这么去形容化除为乘，化除为乘相当于连接多个速算技巧之间的纽带。今天华图教育为大家整理了行测资料分析——化除为乘的进阶运用，希望能对各位考生有所帮助。

比如计算：

首先咱们回忆一下化除为乘的基本用法，当-5%≤r≤5%时，用化除为乘精度比较高。运用环境是在计算现期量1+r时，近似等于现期量/现期量×r。对于上面那个式子，用化除为乘可以将其转化成12345-12345×1%≈12345-123=12222。下面开始拓展：

例题导入

【例1】 ()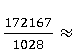

A.163

B.167

C.171

D.174

【解析】选项数量级一致，只需算出多少开头的数就行，所以可以将式子扩大或缩小整十整百倍，换言之可以任意添上一个小数点或者添上百分号，不影响这个数字最后算出来是多少开头的数。

第一步：将分母看作1+2.8%，如此一来这道题就属于化除为乘的范畴，原式化为172167-172167×2.8%。

第二步：优化算法

172167-172167×2.8%≈172167-172167×3%可直接在题目分子上做加减法，省去写式子的过程。减去172167的3%，选项前三位不同，算到第四位即可，原数截位1722，只需要写出1722的1%的三倍就行，1722的1%，就是把这个数的小数点往前移两位，即17.22，取17，它的三倍是一个51，最后只需要计算1722-51=1671。选出1671开头的数B选项。当然可以优化过程，在原式子头上加减，如图：

【例2】()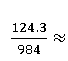

A.12.4%

B.12.6%

C.12.9%

D.13.2%

【解析】第一步：将分母看做98.4%，写成1-1.6%，巧了吧?又是化除为乘的范畴。

第二步：

化除为乘变为124.3x(1+1.6%)，就是在原来的数字上加上124.3×1.6%，1.6%不好算可进行适当估算，计算1.5%即可。先加上这个数的1%，再加上这个数的0.5%。124.3的1%即1.243，取1.2即可。而0.5%就是1%的一半，1.2的一半是0.6，所以要加上1.2再加一个0.6，总的需要加1.8。124.3+1.8即为最终答案126.1。优化过程，直接在原式上加减，如图：

【小结】：今后当碰到分母是95开头至105开头之间的数，就可以将其转化成1+r的形式。

【扩展】：这个方法的精髓就是将分母转化为接近1开头的数，只要距离在1加减5个百分点之间，都可用化除为乘。虽然不一定每次碰到的数字都是这个范围的，但是我们可以创造这个条件。比如：

【例3】 ()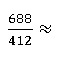

A.1.59

B.1.63

C.1.67

D.1.71

【解析】第一步：将整个分数分子分母同时除以4，可得172103。即可得到分母在105开头以内的数，用例2的思想，将分母看作1+3%，用化除为乘解决它。

第二步：计算172-172×3%。172的1%也就是1.7，3%是1%的三倍，即1.7的三倍是5.1。172-5.1≈167，最终选择167开头的数也就是C选项。你学会了吗?

问题来了，以后咱们如何才能想到这种式子可以用化除为乘呢?

【小结】单看分母的前三位数，当第一位数的5倍>后两位数，就可以先进行约分(如例3的分母412，第一位是4，后两位是12，4×5>12，可以约分)将其化为1开头的数，如果还需要进一步细算，则用上化除为乘即可。还有疑问的小伙伴回到此页第一行，从头开始细品，不要犹豫，你正在进阶，你正在突破，好的方法，你值得拥有!以下是本次内容的思维导图，供大家参考：

　　相关内容推荐：

　　信息汇总——2025国考公告预约 | 职位检索 | 历年进面分数线

　　备考资料——刷题资料 | 网络课程 | 备考图书

　　辅导课程——2025国考系列课程 | 在线咨询

（编辑：华图小土豆）