2023-10-20 15:25:00 文章来源:未知

2024年国考行测数量关系行程问题:与几何问题的纠葛
2024年国考行测数量关系行程问题:与几何问题的纠葛
在公务员行测考试中,几何问题和行程问题这两个知识点的题目属于基本题目也是必考题,它们自己可以单独出题,也可以这两个模块交叉在一起出题,一般交叉在一起利用的是行程的基本知识点,而解决这两个知识点杂糅题目的核心其实更多的倾向与几何问题,今天我们就来聊一聊这一类题目,
【例1】(2019年北京)
下图中ABCD为边长10米的正方形路线,E为AD中点,F为与B相距3米的BC上一点,从E点到F点有小路EGHF,小路的每一段都与AB垂直或平行,且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒,则其以相同速度经EGHF从E点匀速运动到F点用时多少秒?
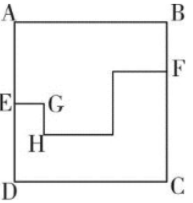
A.12 B.10
C.9 D.8
【华图解析】D。第一步,行程问题,判定求运动时间,时间等于路程/速度,而路程的计算就需要用到几何知识,所以这类题目就是简单的几何和行程问题的杂糅。第二步,E为AD中点,则EA=10÷2=5(米),甲经过EABF从E点到F点所走路程为AE+AB+BF=5+10+3=18(米);标记HF的转弯点为M、N,那么甲经EGHF从E点到F点所走路程为EG+GH+HM+MN+NF=(EG+HM+NF)+GH+MN=10+2+(5+2-3)=16(米)。第三步,两种路线速度相同,路程比为18∶16=9∶8,那么所用时间之比为9∶8,第一种路线用时9秒,那么第二种路线用时8秒。因此,选择D选项。
【例2】(2019年国家)
一个圆形的人工湖,直径为50公里,某游船从码头甲出发,匀速直线行驶30公里到码头乙停留36分钟,然后到与码头甲直线距离为50公里的码头丙,共用时2小时。问该游船从码头甲直线行驶到码头丙需用多长时间?
A.50分钟 B.1小时
C.1小时20分 D.1小时30分
【华图解析】B。第一步,本题考查行程问题,求时间,时间等于路程/速度,而路程的计算就需要用到几何知识,所以这类题目就是简单的几何和行程问题的杂糅。第二步,圆形湖直径为50公里,甲码头到丙码头直线距离为50公里,所以甲丙即为直径。根据性质:在圆里直径与圆周上一点组成的三角形为直角三角形,可知甲乙丙构成一个直角三角形。甲乙=30公里,甲丙=50公里,根据勾股定理可知乙丙=40公里。
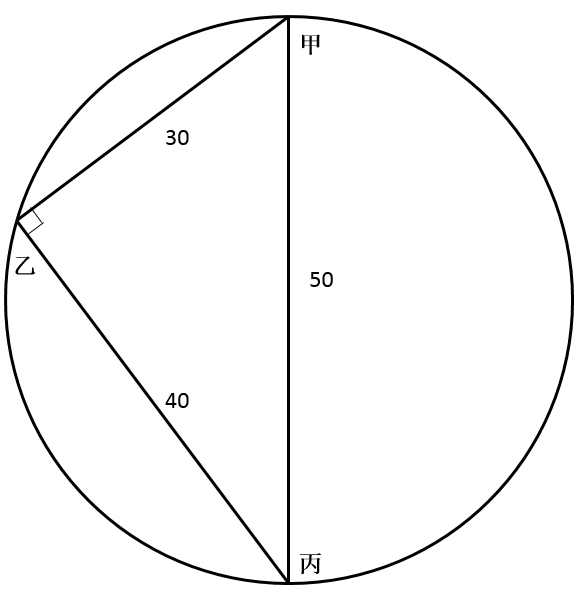

第三步,游船从甲到乙再到丙实际用时120-36=84(分钟),路程30+40=70(公里),而游船从甲直接到丙需要走50公里,用时为(分钟),即1小时。因此,选择B选项。
【例3】(2021年北京)
A地在B地正北方x千米处,甲从A地出发以4千米/小时的速度向南行走,同时乙从B地出发以8千米/小时的速度向西慢跑,出发20分钟后,甲与乙的距离为x千米。问x的值为:
A.5/3 B.6
C.3 D.10/3
【华图解析】D。第一步,本题考查行程问题与几何问题的杂糅。第二步,出发20分钟即1/3小时,甲在此时间内行走距离为4/3千米,乙在此时间内行走距离为8/3千米。如图所示,20分钟后,甲由A行走到A1,BA1的距离为(x-4/3)千米,乙由B慢跑到B1,BB1的距离为8/3千米,根据直角三角形勾股定理有x²=(8/3)²+(x-4/3)²,解得x=10/3。因此,选择D选项。
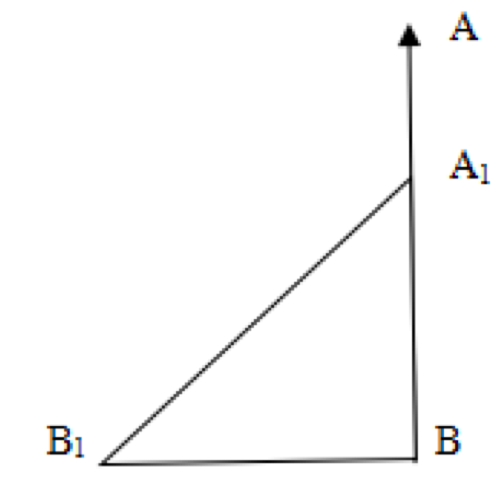
针对这种杂糅题型,目前更多的倾向于考基本的知识点,不过很多需要结合图形做题更简单更好理解,就像我们这三道例题都结合题型来做,所以培养数形结合的思维,从问题入手,找准问题的关键,就能比较容易的解答这类题目。
相关内容推荐:
信息汇总——2025国考公告预约 | 职位检索 | 历年进面分数线
| 职位检索 | 历年进面分数线
辅导课程—— 2025国考系列课程 | 在线咨询
2025国考系列课程 | 在线咨询

企业微信客服

山东华图微信公众号